What are the important tasks?

The answer is "it depends", but here is a post about the Critical Path Method, that helps you recognize the tasks that, if delayed, will make your whole project be late.

When planning a project (specially one with a tight deadline), an important aspect is figuring out which tasks need prioritizing and which don’t. While there may well be a lot of different ways to decide which tasks are important and which aren’t, one way I find particularly interesting is the critical path method. Not only does it seem hard to debate it’s efficacy, but it’s also a method that has a pretty simple algorithm to define what tasks should absolutely be finished on time and which have some wiggle room.

What is the Critical Path Method (CPM)?

The CPM is based on the realization that for many projects there is only a subset of tasks that define the project’s duration. That is: you can’t postpone any of those tasks without affecting the project’s end-date. Here a simple example might be useful. Suppose a project has the following diagram:

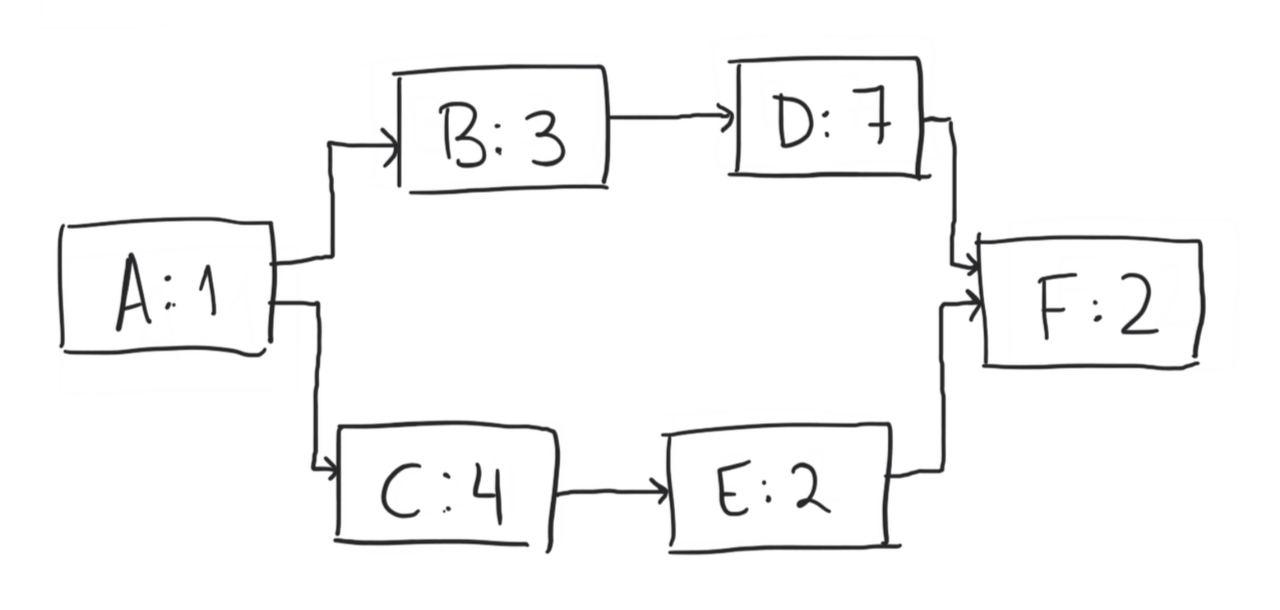
Where each rectangle represents a task, the letter before the colon is the task label, and the number after the colon is the expected duration in days. Two tasks are linked by an arrow if the first is a prerequisite of the second. Lets see what happens when we try to create the tightest possible schedule for our set of tasks…

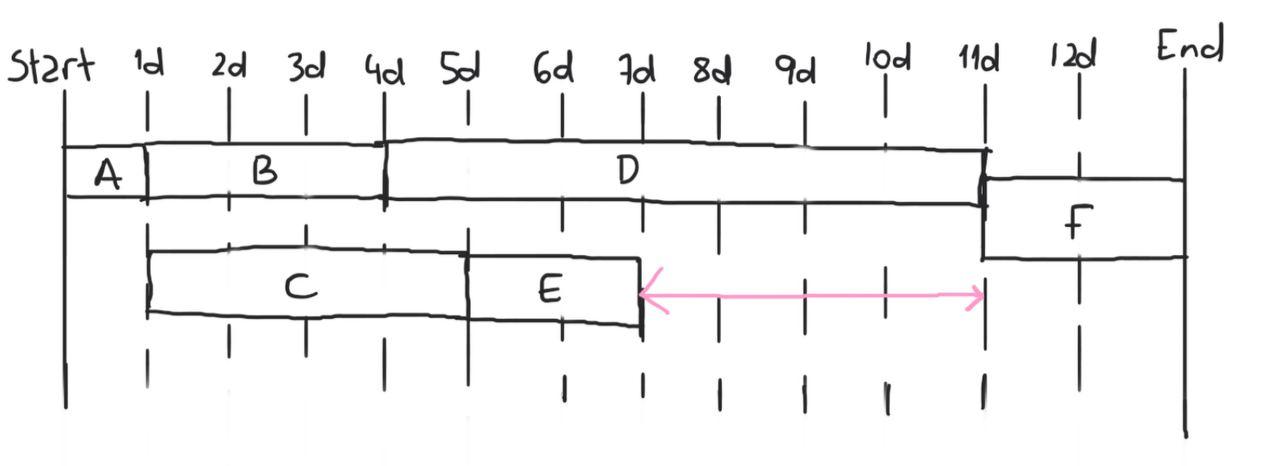
See how we can change the start date of tasks C and E by up to 4 days, or even take longer performing them, without needing to move the ‘End’ line? But if task B, for example, is late then the whole project gets pushed back. Conversely, we cannot pull the end-date sooner without either reducing the duration, or starting earlier on, tasks A, B, D, and F. These 4 tasks are our critical path. They must absolutely be done in time if we don’t want to delay the end of the project.

A nice little algorithm for finding the critical path of a project

The idea behing the algorithm is to first set the earliest possible start-date for each task, then set the latest possible start-date that doesn’t alter the duration of the task (i.e. the latest possible start-date of the last class is equal to its earliest possible start-date). The critical path is made by all the tasks for which the earliest and latest start-date are the same.

An interesting thing about this algorithm is that we set the earliest start-dates from the earlier tasks to the latter, and we set the latest start dates from the latter to the earliest. That is because we look to the prerequisites of a task to see when is the earliest that they will finish, and then we define how early the task can start based on that: it can start as soon as the last prerequisite is done. To set the latest start-date, however, we look at the latest that tasks coming after if can start, and we find out what is the latest that it can start so that it doesn’t delay any of the tasks that depend on it.

In Python and with some OOP:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Task:
    def __init__(self, duration: int, prerequisites: [Task]):
        self.earliest_start_date = None
        self.latest_start_date = None

        self.duration = duration

        self.prerequisites = prerequisites
        self.postrequisites = []

        for prerequisite in self.prerequisites:
            prerequisite.add_postrequisite(self)
    
    def set_earliest_start_date(self):
        self.earliest_start_date = self.project.start_date
        for prerequisite in self.prerequisites:
            if prerequisite.earliest_start_date is None:
                prerequisite.set_earliest_start_date_recursive()
            self.earliest_start_date = max(
                self.earliest_start_date,
                prerequisite.earliest_start_date + prerequisite.planned_duration,
            )

    def set_latest_start_date(self):
        self.latest_start_date = self.earliest_start_date + timedelta(days=999999)
        for postrequisite in self.postrequisites:
            if postrequisite.latest_start_date is None:
                postrequisite.set_latest_start_date_recursive()
            self.latest_start_date = min(
                self.latest_start_date,
                postrequisite.latest_start_date - self.planned_duration,
            )
        if len(self.postrequisites) == 0:
            self.latest_start_date = self.earliest_start_date

We define a task as having a duration and a set of prerequisites. We also make it have a list of all the tasks that have itself as a prerequisite (we call those it’s postrequisites, though I suspect the term isn’t quite right here!). This second list will help us when defining the latest start-date. The idea of the algorithm is that the earliest a task can start is the last day of one of it’s prerequisites, and the latest a task can start is the first day of one of it’s postrequisites. The first task can start, at the earliest, on day 0, and the last task cannot end after the task that has the latest earliest-end-date (earliest-start-date + duration), otherwise it would delay the end of the project. This is a recursive implementation where when we want to set an earliest start-date (or latest) for a task, we look at it’s prerequisites (or postrequisites). If their earliest start-date is not set, then we recursively set those. If their end-date is later than what we consider to be the tasks earliest start-date, then we push back the task to start at the earliest at this prerequisite’s end-date.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Project:
    def __init__(self, tasks):
        self.tasks = tasks
    
    def get_critical_path(self):
        for task in self.tasks:
            if len(task.postrequisites) == 0:
                task.set_earliest_start_date_recursive()
        for task in self.tasks:
            if len(task.prerequisites) == 0:
                task.set_latest_start_date_recursive()

        return sorted(
            [
                task 
                for task in self.tasks 
                if task.earliest_start_date == task.latest_start_date
            ], 
            key=lambda task: task.earliest_start_date
        )

Our project here is just a list of tasks. The critical path is found by setting the earliest start-dates for all the tasks that have no postrequisites, then the latest start-dates for the tasks that have no prerequisite. Because we use a recursive approach, by setting the tasks from each end of the “chronogram”, we know that they will recursively set their prerequisites, which will set their prerequisites, and so on, such that all tasks will be set. Then we return the tasks for which earliest_start_date == latest_start_date.

Bonus: Recursive vs. Iterative

Because we’re programming in Python here, an obvious question might be why implement the algorithm recursively rather than iteratively (which should be faster to run!). Well, one thing is that both “paradigms” have their own more-intuitive version of the algorithm: recursively we start at the end, knowing that recursivity will get to the beginning and back, while iteratively we start at the beginning and move forwards. I tested the implementation of these two ideas, and recursivity was much faster by a high margin (0.13s vs 4.8s on a project with 1000 tasks). The reason for that, I believe, is that in the recursive approach we don’t need to keep track of what tasks we have already set the start-dates for, and which tasks we can set the start-date for. This means not only two less data structures to keep and update, but also knowing that a task can now have it’s start-date set is an operation that takes O(n) time, since we need to look at all it’s prerequisites/postrequisites, and since everytime we set it for a task we need to look at all tasks we expect have been “freed”, which are the postrequisites/prerequisites of the task we just set the start-date for, this is something that takes O(n^2) time. But is done for every task, so ultimately the algorithm ends up being O(n^3). This is maybe something that can be optimized to remain in the O(n^2) time, but it probably would require some bizarro code choices that would damage code readability and maintanability (as well as elegance, though that matters much less).

But recursivity iteratively?

That all said, the recursive algorithm could be implemented iteratively, and in that case it might perform better. However, it would still require some not-so-nice design choices that could make it harder to read and understand. Considering that on a project with 1000 tasks (probably a lot more than is realistic for a real-life scenario) had the critical path found in 0.13s, this implementation is more than fine.

A P.S. on the iterative solution:

The iterative solution is actully analogous to Kahn’s algorithm for topological sorting of a Directed Acyclical Graph (DAG) – note that out tasks can be seen as a directed acyclical graph, as a cycle in our scenario represents a deadlock: two tasks that cannot be done before the other is done. In Kahn’s algorithm the nodes of the graph (our tasks) are taken and placed into a list. In our case this is not necessary, as we don’t really need the sorting afterwards, so we can just set the dates as we go. Another way to think about this is that we could first use Kahn’s algorithm to generate a topological sorting of the tasks, and then set the start-dates for those tasks following the sorting. However, because the tasks are added to the sorted list already in order, instead of addin them to a sorted list we can, as we do, simply set the start-dates when we would add them to the list.